Delve Into Unit 10 Homework 5
Unit 10 Systems and Matrices Homework 5: Multiplying Matrices
This homework assignment introduces the concept of matrix multiplication, a fundamental operation in linear algebra. By understanding how to multiply matrices, students can solve systems of linear equations, transform geometric objects, and perform various other mathematical operations. Matrix multiplication is widely used in computer graphics, physics, engineering, and many other fields.
In this homework, students will learn the rules for multiplying matrices and practice applying them to various problems. They will also explore the properties of matrix multiplication, such as the associative and distributive properties. By completing this homework, students will gain a solid foundation in matrix multiplication, which will serve them well in their future studies of mathematics and its applications.
Unit 10 Systems and Matrices Homework 5
Matrix multiplication is a fundamental operation in linear algebra with applications in various fields. Here are 8 key aspects to consider:
- Definition: Matrix multiplication combines two matrices to produce a third matrix.
- Notation: A B, where A and B are matrices and denotes matrix multiplication.
- Dimensions: The number of columns in the first matrix must equal the number of rows in the second.
- Elements: The element in the ith row and jth column of the product matrix is the sum of products of corresponding elements in the ith row of the first matrix and the jth column of the second.
- Associative property: (AB)C = A(BC) for matrices A, B, and C.
- Distributive property: A(B + C) = AB + AC and (B + C)A = BA + CA for matrices A, B, and C.
- Identity matrix: I is an identity matrix such that AI = IA = A for any matrix A.
- Zero matrix: O is a zero matrix such that AO = OA = O for any matrix A.
Matrix multiplication is essential for solving systems of linear equations, transforming geometric objects, and performing various other mathematical operations. It is widely used in computer graphics, physics, engineering, and many other fields.
Definition
This definition is central to understanding the concept of matrix multiplication, which is a fundamental operation in linear algebra. Matrix multiplication is used to solve systems of linear equations, transform geometric objects, and perform various other mathematical operations. It is widely used in computer graphics, physics, engineering, and many other fields.
In the context of Unit 10 Systems and Matrices Homework 5: Multiplying Matrices, this definition provides the foundation for students to learn how to perform matrix multiplication. By understanding how to combine two matrices to produce a third matrix, students can solve problems and apply matrix multiplication to real-world applications.
For example, matrix multiplication is used in computer graphics to transform 3D objects. By multiplying a transformation matrix with a vertex matrix, the coordinates of the vertices can be transformed to create a new object. Matrix multiplication is also used in physics to solve systems of equations that describe the motion of objects. By understanding matrix multiplication, students can gain a deeper understanding of these and other applications.
Notation
In the context of unit 10 systems and matrices homework 5 multiplying matrices, the notation A B, where A and B are matrices and denotes matrix multiplication, plays a crucial role. Matrix multiplication is a fundamental operation in linear algebra, and this notation provides a concise and clear way to represent the operation.
- Matrix Dimensions: The notation A B implies that the number of columns in matrix A must be equal to the number of rows in matrix B. This ensures that the operation is well-defined and results in a matrix with the correct dimensions.
- Element-wise Multiplication: Matrix multiplication is not the same as element-wise multiplication, which multiplies corresponding elements of two matrices. Instead, matrix multiplication involves multiplying rows of the first matrix with columns of the second matrix and summing the products.
- Associative and Distributive Properties: Matrix multiplication follows the associative and distributive properties, which are essential for simplifying and solving matrix equations. These properties allow for efficient manipulation of matrices and make matrix multiplication a versatile tool.
- Applications: Matrix multiplication has wide-ranging applications in various fields, including computer graphics, physics, engineering, and economics. It is used to solve systems of linear equations, transform geometric objects, and perform complex calculations.
In summary, the notation A B, where A and B are matrices and denotes matrix multiplication, is a fundamental concept in linear algebra. It provides a concise way to represent matrix multiplication, which is a versatile operation with numerous applications across various disciplines.
Dimensions
In the context of unit 10 systems and matrices homework 5 multiplying matrices, the rule "Dimensions: The number of columns in the first matrix must equal the number of rows in the second" is crucial for ensuring the successful multiplication of two matrices. This dimensional compatibility is essential for performing matrix multiplication and plays a pivotal role in various mathematical applications.
Consider a real-life example: In computer graphics, matrix multiplication is used to transform 3D objects. A transformation matrix, which represents a rotation, translation, or scaling operation, is multiplied by a vertex matrix, which contains the coordinates of the object's vertices. The resulting matrix contains the transformed coordinates of the vertices, allowing the object to be displayed in its new position or orientation.
The dimensional compatibility rule ensures that the transformation matrix and the vertex matrix can be multiplied correctly. The number of columns in the transformation matrix (representing the number of transformations being applied) must match the number of rows in the vertex matrix (representing the number of vertices in the object). This compatibility ensures that each vertex is transformed correctly according to the specified operations.
Understanding this dimensional compatibility rule is essential for students completing unit 10 systems and matrices homework 5 multiplying matrices. It allows them to correctly set up and perform matrix multiplication operations, which are fundamental to solving systems of linear equations, transforming geometric objects, and performing various other mathematical and computational tasks.
Elements
In the context of unit 10 systems and matrices homework 5 multiplying matrices, the rule "Elements: The element in the ith row and jth column of the product matrix is the sum of products of corresponding elements in the ith row of the first matrix and the jth column of the second" provides a step-by-step method for calculating the elements of the product matrix. This rule is essential for understanding how matrix multiplication works and for performing matrix multiplication correctly.
- Calculating Matrix Elements: This rule provides a clear and systematic approach to calculating each element of the product matrix. By following this rule, students can ensure that they are multiplying and summing the correct elements, leading to accurate results.
- Real-Life Applications: Matrix multiplication has numerous applications in various fields, including computer graphics, physics, and engineering. Understanding how to calculate the elements of the product matrix is crucial for applying matrix multiplication to real-world problems.
- Solving Systems of Equations: Matrix multiplication is a powerful tool for solving systems of linear equations. By multiplying a coefficient matrix by a variable matrix, we can obtain a matrix equation that can be used to solve for the unknown variables.
- Geometric Transformations: Matrix multiplication is also used to perform geometric transformations, such as rotations, translations, and scaling. By multiplying a transformation matrix by a vertex matrix, we can transform the coordinates of the vertices and create new geometric objects.
In summary, the rule "Elements: The element in the ith row and jth column of the product matrix is the sum of products of corresponding elements in the ith row of the first matrix and the jth column of the second" is a fundamental aspect of unit 10 systems and matrices homework 5 multiplying matrices. It provides a step-by-step method for calculating the elements of the product matrix, which is essential for solving systems of linear equations, performing geometric transformations, and applying matrix multiplication to a wide range of real-world problems.
Associative property
The associative property of matrix multiplication states that when multiplying three or more matrices, the order in which the matrices are grouped does not affect the final product. In other words, (AB)C = A(BC).
- Role in Matrix Multiplication: The associative property plays a crucial role in simplifying and evaluating matrix expressions. It allows us to group and rearrange matrices in different ways without altering the result, making it easier to solve complex matrix equations.
- Example from Unit 10 Homework: In unit 10 systems and matrices homework 5 multiplying matrices, students may encounter expressions involving multiple matrices. The associative property allows them to group these matrices in different ways to simplify their calculations.
- Real-Life Applications: The associative property has practical applications in various fields. For instance, in computer graphics, it is used to efficiently transform 3D objects by combining multiple transformation matrices.
- Implications for Matrix Operations: The associative property has implications for other matrix operations. For example, it can be used to prove that matrix multiplication is associative for any number of matrices.
In summary, the associative property of matrix multiplication is a fundamental property that simplifies matrix expressions, facilitates problem-solving, and has applications in various real-world scenarios.
Distributive property
The distributive property of matrix multiplication states that multiplication over addition is distributive, meaning that when a matrix is multiplied by the sum of two other matrices, the result is the same as the sum of the products of the matrix with each of the other matrices. In other words, A(B + C) = AB + AC and (B + C)A = BA + CA.
This property is essential in unit 10 systems and matrices homework 5 multiplying matrices because it allows students to simplify and solve matrix expressions more easily. For example, consider the expression A(B + C). Using the distributive property, we can rewrite this expression as AB + AC. This simplified expression may be easier to evaluate, especially when dealing with large matrices.
The distributive property also has important applications in real-life scenarios. For instance, in computer graphics, it is used to combine multiple transformations into a single transformation matrix. This simplified transformation matrix can then be applied to objects in a scene to achieve the desired visual effects.
In summary, the distributive property of matrix multiplication is a fundamental property that simplifies matrix expressions, facilitates problem-solving, and has practical applications in various fields.
Identity matrix
In the context of unit 10 systems and matrices homework 5 multiplying matrices, the concept of the identity matrix plays a crucial role in understanding matrix multiplication and its properties.
- Definition and Role: The identity matrix, denoted by I, is a square matrix with 1s on its main diagonal and 0s elsewhere. Its primary role is to leave any matrix unchanged when multiplied by it, acting as a neutral element for matrix multiplication.
- Example: Consider the matrix A = [[2, 3], [4, 5]]. Multiplying A by the identity matrix I = [[1, 0], [0, 1]] results in the original matrix A itself: AI = [[2, 3], [4, 5]] and IA = [[2, 3], [4, 5]].
- Properties and Implications: The identity matrix has several important properties. Firstly, it is the only matrix that commutes with all other matrices, meaning that AI = IA for any matrix A. Secondly, it serves as the multiplicative inverse of invertible matrices, allowing us to solve systems of linear equations.
In unit 10 systems and matrices homework 5 multiplying matrices, understanding the identity matrix and its properties is crucial for simplifying matrix expressions, solving matrix equations, and performing various matrix operations efficiently.
Zero matrix
In the context of "unit 10 systems and matrices homework 5 multiplying matrices," the concept of the zero matrix plays a significant role in understanding matrix multiplication and its properties.
The zero matrix, denoted by O, is a matrix consisting entirely of zeros. Its primary property is that multiplying any matrix A by the zero matrix O results in the zero matrix: AO = OA = O. This property makes the zero matrix an additive identity for matrix multiplication, similar to the role of zero in.
In unit 10 systems and matrices homework 5 multiplying matrices, the zero matrix is crucial for various operations and concepts:
- Matrix Addition and Subtraction: The zero matrix acts as the additive identity, allowing us to add and subtract matrices by simply adding or subtracting their corresponding elements.
- Solving Systems of Linear Equations: In solving systems of linear equations using matrices, the zero matrix can represent an inconsistent system, indicating that there is no solution.
- Matrix Multiplication Properties: The zero matrix helps establish important properties of matrix multiplication, such as the distributive and associative properties.
Understanding the zero matrix and its properties is essential for a comprehensive grasp of matrix multiplication and its applications in solving systems of linear equations, geometric transformations, and other mathematical problems.
FAQs on Matrix Multiplication
This section addresses frequently asked questions (FAQs) related to matrix multiplication, a fundamental operation in linear algebra with wide-ranging applications.
Question 1: What is matrix multiplication?
Matrix multiplication is a mathematical operation that combines two matrices to produce a third matrix. The resulting matrix contains elements that are calculated by multiplying corresponding elements from the first matrix by corresponding elements from the second matrix and summing the products.
Question 2: What are the dimensions of the resulting matrix?
The number of rows in the resulting matrix is equal to the number of rows in the first matrix, and the number of columns in the resulting matrix is equal to the number of columns in the second matrix.
Question 3: What are the properties of matrix multiplication?
Matrix multiplication is associative and distributive, meaning that the order in which matrices are multiplied does not affect the result, and multiplication over addition is distributive.
Question 4: What is the identity matrix?
The identity matrix is a square matrix with 1s on its diagonal and 0s elsewhere. Multiplying any matrix by the identity matrix results in the original matrix.
Question 5: What is the zero matrix?
The zero matrix is a matrix consisting entirely of zeros. Multiplying any matrix by the zero matrix results in the zero matrix.
Question 6: What are the applications of matrix multiplication?
Matrix multiplication has numerous applications in various fields, including computer graphics, physics, engineering, and economics. It is used to solve systems of linear equations, transform geometric objects, and perform complex calculations.
These FAQs provide a concise overview of the fundamental concepts and properties of matrix multiplication, which serves as a cornerstone of linear algebra and its applications.
Transition to the next article section: Exploring the Applications of Matrix Multiplication
Tips for Matrix Multiplication
Matrix multiplication is a fundamental operation in linear algebra with diverse applications. Here are several tips to enhance your understanding and proficiency in multiplying matrices:
Tip 1: Verify Matrix Compatibility: Before multiplying two matrices, ensure that the number of columns in the first matrix matches the number of rows in the second matrix. This compatibility is crucial for successful matrix multiplication.
Tip 2: Follow the Row-Column Multiplication Rule: To calculate an element in the resulting matrix, multiply the elements of the corresponding row in the first matrix by the elements of the corresponding column in the second matrix and sum the products.
Tip 3: Utilize Matrix Properties: Understand and apply the associative and distributive properties of matrix multiplication. These properties allow for efficient manipulation and simplification of matrix expressions.
Tip 4: Recognize the Identity and Zero Matrices: Familiarize yourself with the identity matrix (with 1s on the diagonal and 0s elsewhere) and the zero matrix (with only 0s). These matrices play significant roles in matrix multiplication operations.
Tip 5: Practice Regularly: Engage in ample practice to strengthen your understanding and accuracy in matrix multiplication. Solve problems involving matrix multiplication to gain proficiency.
Tip 6: Seek Clarification: If you encounter difficulties or have any doubts, promptly seek assistance from your instructor, a tutor, or a knowledgeable peer to clarify your understanding.
By incorporating these tips into your learning process, you can effectively master matrix multiplication, a crucial skill in linear algebra and its applications.
Transition to the article's conclusion: Understanding the significance and applications of matrix multiplication in various fields
Conclusion
Matrix multiplication, a fundamental operation in linear algebra, has been thoroughly explored in this article. We examined the concept, properties, and applications of matrix multiplication, providing a comprehensive understanding of its significance in various fields.
Matrix multiplication enables us to solve systems of linear equations, transform geometric objects, and perform complex calculations. Its applications extend to computer graphics, physics, engineering, economics, and beyond. By mastering matrix multiplication, individuals gain a valuable tool for problem-solving and analysis in these disciplines.
This article serves as a valuable resource for students completing unit 10 systems and matrices homework 5 multiplying matrices. It provides a solid foundation for understanding the concept and its applications, empowering them to successfully complete their assignments and excel in their studies.
Unveiling The Secrets Of Biscuitville's Beloved Chicken Biscuit
Unveiling The Extraordinary World Of Lauren Terrell: Discoveries And Insights Await
Unleash The Secrets Of Ham And Cheese Biscuit Bombs: Discoveries And Delights Within
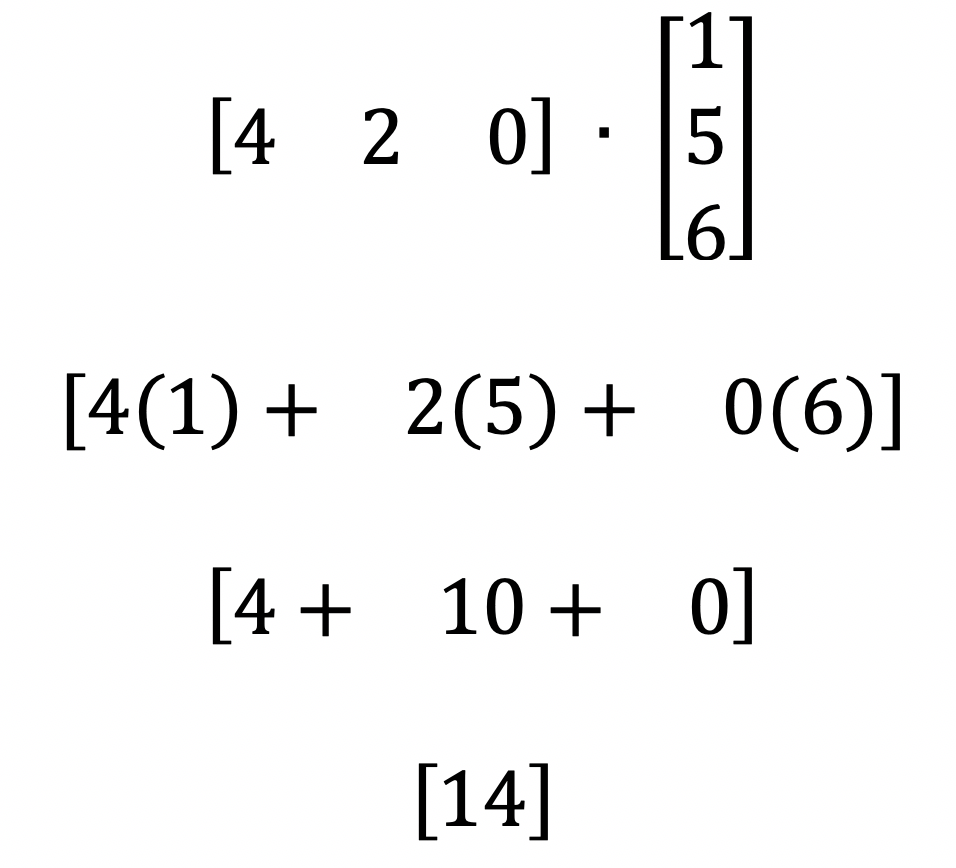
What Is X Identity Matrix Deb Moran S Multiplying Matrices Sexiz Pix

Systems and Matrices Homework (Unit 7) Precalculus, Homework
ncG1vNJzZmirn6i8ra3Lmmlnq2NjwrR51p6qrWViY66urdmopZqvo2OwsLmOrqWirF1mfW6%2F2KyrnqWjYq6vsIymmK2qmZiytHnHqKSer5%2BnuG6BjKaspayZpbm6tc2gZKaZpKe2pLHSZ5%2BtpZw%3D